Abstract

Electrochemistry is the process of oxidation-reduction reactions that produce electrochemical reactions and is the intersection between chemistry and electricity. In electrochemistry, electrons are transferred as a result of oxidation-reduction reactions, meaning that a chemical reaction results in electrical movement. Electrochemistry is an applicable concept in a multitude of fields, one being neural activity. Oxidation-reduction reactions mediate neural communication, playing a crucial role in the facilitation of overall neural processes. An equation to quantify and define the electrochemical equilibrium between the concentration gradient and the electrical potential for a certain ion is the Nernst equation. The regulation of the concentration gradient and electrical potential is done through reversal potential^3, and can be calculated through given concentrations of the particular ion.

1. Introduction of the Nernst Equation and Action Potential

The Nernst equation is utilized as a quantitative demonstration of concentrations of an ion that exists on either side of the membrane⁷. The potential difference in concentration of these ions is classified as the “voltage”, and can be measured when the membrane is in equilibrium. With this said, an action potential is a rapid change in the voltage, or concentration of a particular ion, across a neuron membrane. The function of the action potential is to transmit information across the brain by utilizing the axons located within the white matter of the brain. This process of action potential can be determined by the relative ratio of ions existing on either side of the membrane, which is where the Nernst Equation can be applied. Referring to the images below, the first equation is the general Nernst equation, while the equation on the right is applied in action potential within neurons. Action potentials occur within 1 millisecond, making it a very fast reaction². In addition to this, action potentials are considered as an all-or-nothing action, so the voltage of the neurons have to meet a certain threshold in order for the information to be transmitted across neurons. A figure depicting this concept is found in Section III.

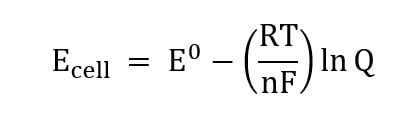
Figures 1 and 2 – the general Nernst Equation and the Nernst Equation in Action Potential, Respectively.

2. Analysis of the Nernst Equation

As can be seen in the first equation on the left, the voltage of the cell (E_cell) is equal to the standard voltage potential (E⁰) subtracted by the entirety of the gas constant (8.314 J/mol^-1k^-1) times temperature (Kelvin) divided by the number of electrons transferred multiplied by Faraday’s constant (96485 C/mol) and finally multiplied by the natural log of the Q, the concentration of products divided by the concentration of reactants. The standard voltage is obtained by determining the standard reduction potential at the anode and subtracting this value by the standard reduction potential of reduction at the cathode. Often, the value of RT in the original Nernst equation is simplified to 0.0591/n since R and F are constants, while the temperature (T) is typically 298 K, which is 25 degrees Celsius. The derivation of the Nernst equation comes from Gibbs Free Energy (ΔG), which is the change in the enthalpy – the change in the amount of heat in a process. Simply put, this Gibbs Free Energy equation contains the state functions of thermodynamics values. The original equation is written as  ΔG = ΔG^o + RTlnQ, and this equation can be rewritten by substituting known values that are equal to one another, which are ΔG = -nFEcell and ΔG^o = -nFE^ocell. The resulting equation is -nFEcell = -nFE^ocell + RTlnQ. Upon dividing both sides by -nF, the Nernst Equation is created.

3. The Integration of the Nernst Equation in Neuron Physiology A) Introduction to the Neural Membrane

The concentrations that mediate the voltage in a neuron are sodium (Na⁺), potassium (K⁺), and chloride (Cl^–)¹. The extracellular region has a high concentration of Na⁺ and Cl^–, while there is a low concentration of K⁺. Intracellularly, there is only a high concentration of K⁺ and a low concentration of Na⁺ and Cl^–. These concentrations are mediated through an active ion pump, with the most common one being the Na⁺/K⁺ pump. This pump requires energy, and Na⁺ tends to depolarize the cell (makes the intracellular area more positive), K⁺ hyperpolarizes the cell (makes the intracellular area more negative), and Cl^– hyperpolarizes the cell. These differences in concentrations across a semipermeable membrane creates an electrical potential, which can be portrayed through the equation mentioned previously¹:

B) Determining Voltage Potential and Exploring Driving Force

The Nernst equation focuses on individual ion concentrations, so the Nernst equation is typically applied towards Na⁺, K⁺, and Cl^–. The concentrations exist as milliMolar and the concentration of the selected ion outside of the membrane is divided by the concentration of the ion inside the membrane. As with the typical application of Nernst equation, the greater amount of the ion inside the cell signifies a lower voltage. The reversal potential of Na⁺ – the value where there is no net flux – has a reversal potential of +59mV, -65mV for Cl^–, and -80mV for K⁺³. This means that these are the values that these ions try to reach in order to reach equilibrium potential. When there is depolarization across the neuron and there is a signal sent for the voltage-gated channels to open⁴, the difference between the membrane potential and the reversal potential of a certain ion will determine the electrochemical driving force (V_df)⁶. This driving force is what causes the ions to move down its own electrochemical gradient. This magnitude of the electrochemical driving force determines how far an ion is from reaching an equilibrium.

V_df = V_m – V_eq

C) Occurrence of Depolarization – Signal Transmission

Image taken from https://jackwestin.com/resources/mcat-content/nerve-cell/action-potential

 As can be seen in the figure above, the typical voltage of the resting potential is -0.70 mV, meaning that there are more sodium ions inside the cell than there are potassium ions within the cell. Moreover, this means that an external force is required to create the potential and send it through the neuron. With this positive value of the voltage, then the change in Gibbs Free Energy (ΔG) is positive, which means that the reaction of a neuron is not spontaneous. When there is a depolarization inside the cell, voltage-gated Na⁺ channels open, allowing Na⁺ into the cell (depolarizing the cell) and therefore continuing the propagation of the signal. This creates the voltage potential that can then be quantified through the Nernst equation. At the maximum voltage (peak action potential), the voltage is typically measured to be +30mV. When the neuron goes through the process of repolarization, the intracellular area is becoming more negative, meaning that ions such as the Na⁺ is exiting and making their way to the extracellular space. This flux of ions is not precise, however, so the membrane typically overshoots and reaches a “hyperpolarized” state, meaning that there are too many polarizing ions intracellularly and has reached a voltage below its typical equilibrium resting state.

4. How Action Potential is Measured in a Neuron

In order to determine the voltage of the neuron, two microelectrodes are typically inserted into the neuron, with one connected to a stimulator while the other one is connected to a voltmeter to measure the voltage². The electrode stimulator is often connected to a battery, which corroborates the idea that an external energetic force needs to be applied to the battery in order for an action potential to occur. This electrode stimulator can either add a positive voltage or negative voltage to the neuron, showing the depolarizations and polarizations of the neuron.

5. Applying the Nernst Equation in Action Potential A) Benefits of its Applications

The Nernst equation, as has been covered, is able to be used to measure the exact value of the change of the equilibrium potential. As a result, a person is able to determine the cell potential even under non-standard conditions. At a broader application, the complexities of the brain are able to start being understood using this Nernst Equation. Decades of research have been in work to determine which areas of the brain mediate certain actions. For instance, motor control can be linked to the motor cortex within the brain, but to potentially figure out lesser known connections that dictate a certain behavior/action, calculating the polarization – or lack thereof – of a neural membrane in a certain area of the brain can be used as a way to corroborate that a certain area is responsible for a given action/behavior. Because of this, the Nernst Equation can be used in research and discovering neuroanatomical regions responsible for mediating certain behaviors. 

B) Shortcomings of its Applications

The downfall of the Nernst Equation is that it only shows the concentrations of one ion that is altering its concentration across the membrane, but multiple ions play a role in membrane potential⁵. This means that, although the equation can be applied effectively for finding the equilibrium, the equation is not as reliable when there are multiple voltage-gated channels that are responsible for mediating the polarization – and therefore the transfer of a message – of a neuron^5. Because scientists are aware of the limitations of the Nernst Equation, an equation was created for when a membrane is permeable to more than one ion. As previously mentioned, K⁺ and Na⁺ play crucial roles in the polarization and depolarization, respectively. This equation is known as the Goldman-Hodgkin and Katz (GHK) equation².

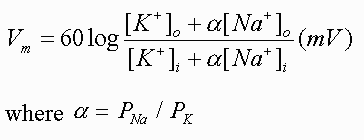
The GHK Equation, with alpha signifying the ratio of Na⁺ permeability to K⁺ permeability.

This equation transforms into the Nernst Equilibrium potential if there is a lack of presence of either ion within this equation. The permeability portion (α) is important in determining voltage since a membrane can be one-hundred times more permeable to K⁺ than Na⁺ or vice versa, meaning that much more of that given ion would travel across the membrane, making it an uneven diffusion of the ions even if the concentrations of these ions are the same².

6. Concluding Remarks

As has been explained throughout the paper, the Nernst Equation is an effective way to measure the voltage of the neurons during an action potential. The action potential is the process by which neurons transmit information, which is an integration of both chemical and electrical signaling. The action potentials are able to be compared to an electrolytic cell, because it requires an external input of energy into the neuron in order for an action potential to occur. Since specific ions are able to either polarize or depolarize the cell – which dictates the action potential – the Nernst Equation measures the concentrations of an ion being diffused against a selectively permeable membrane and the initial voltage of the cell (which typically hovers around -70mV) to calculate the voltage of the membrane. The voltage of the cell can be calculated whether in equilibrium or not in equilibrium. Moreover, the driving force of a particular ion can also be considered to determine which space – whether extracellular or intracellular – the ion will try to go to in order to maintain equilibrium. However, the Nernst Equation is not as applicable when a membrane is selectively permeable to more than one membrane, so the GHK Equation is applied instead in this circumstance. It is important to know the voltage of certain neurons in order to determine which neuroanatomical regions mediate certain behaviors/actions. To conclude, the Nernst Equation is crucial to determine the voltage of a membrane when this membrane is only selectively permeable for one ion.

7. References

1. Braun, J. (n.d.). Theoretical neuroscience I lecture 6: Synaptic conductances. Theoretical Neuroscience Part I. https://bernstein-network.de/wp-content/uploads/2021/02/01_Lecture-01-Nernst-equation.pdf
2. Byrne, J. H. (2021). Resting potentials and action potentials (Section 1, Chapter 1) Neuroscience Online: An electronic textbook for the Neurosciences: Department of Neurobiology and Anatomy – the University of Texas Medical School at Houston. Resting Potentials and Action Potentials (Section 1, Chapter 1) Neuroscience Online: An Electronic Textbook for the Neurosciences | Department of Neurobiology and Anatomy – The University of Texas Medical School at Houston. https://nba.uth.tmc.edu/neuroscience/m/s1/chapter01.html#:~:text=One%20can%20use%20the%20Nernst,changes%20by%20about%2015%20mV
3. Fitzakerley, J. (2014, September 20). 2014 Ion Channel Physiology. Equilibrium potentials. https://www.d.umn.edu/~jfitzake/Lectures/DMED/IonChannelPhysiology/MembranePotentials/EquilibriumPotentials.html#:~:text=Equilibrium%20(or%20reversal)%20potentials&text=Erev%20can%20be%20calculated,K%2B%20is%20~%2D88%20mV.&text=for%20a%20given%20ion%2C%20the,R%20%3D%20gas%20constant
4. Grider, M. H., Jessu, R., & Kabir, R. (2022, May 15). Physiology, action potential – statpearls – NCBI bookshelf. Physiology, Action Potential. https://www.ncbi.nlm.nih.gov/books/NBK538143/
5. National Library of Medicine. (2001). Molecular biology of the cell – NCBI bookshelf. Voltage-Gated Ion Channels. https://www.ncbi.nlm.nih.gov/books/NBK21054/
6. PhysiologyWeb. (2015, February 15). Electrochemical driving force acting on ions – resting membrane potential. Resting Membrane Potential. https://www.physiologyweb.com/lecture_notes/resting_membrane_potential/resting_membrane_potential_electrochemical_driving_force_acting_on_ions.html#:~:text=The%20driving%20force%20is%20the,ion%20is%20from%20its%20equilibrium
7. TeachMePhysiology. (2021, August 23). Resting membrane potential – nernst – generation. Resting Membrane Potential. https://teachmephysiology.com/nervous-system/synapses/resting-membrane-potential/#:~:text=Nernst%20Equation,-The%20Nernst%20equation&text=where%20Vm%20%3D%20equilibrium%20potential,inside%20the%20cell%20%5Bmol%5D